Originally posted: 09/20/2017

In this post, I’ll shed some light on how JavaScript handles its numbers. We will go down to the binary and back up.

Why write about numbers in JavaScript?

It seems to be common knowledge that JavaScript has a single and unpredictable number type, 64-bit floating point. Watch out! But, whenever I look for more information on what to watch out for,I see the exact same example:

> 0.1 + 0.2
  0.30000000000000004

Okay. JavaScript’s weird? I guess. But why does it do that? By the end of this post, hopefully it’ll be clear exactly how JavaScript internally represents numbers in binary and how that causes this result to be perfectly reasonable to a JavaScript engine.

Where might number-related inconsistencies appear in our code?

Anywhere. I’ve come across three distinct instances this past year.

1. Last February, I was building a data visualization for mobile phone subscriptions in North Africa. The dataset ran from 1980–2014. As you can imagine, the number of mobile phone subscriptions per 100,000 persons in North Africa in 1980 were miniscule. In fact, they were so tiny that when calculating the SVG coordinates using d3.js’ .line() method, it returned NaN. Weird.

2. This past June, I was attempting to convert a string to a number as part of a LeetCode challenge. I couldn’t consistently convert an “integer string” (string made up of integer values) into a number if it was over 16 digits. I wrote a blog post, leaving out the binary, focusing on the fact that you should expect unexpected results when working with numbers over 16 digits, big or small.

3. Last weekend, I participated in a mock interview. The question was how to find the square root of a number without using Math.sqrt(). After writing a binary search function, the interviewer asked for me to walk through the function when the input is equal to 2,000,000. Part of that function takes 1,000,000 (the midpoint) and multiplies it by itself (or x², where x is the input). Which, won’t work in some number systems, but I thought it might just work in 64-bit floating point. It is less than the magical 16 digit mark!

This is just a small number anecdotal experiences from an early career front-end dev who doesn’t work with large amounts of data regularly. I am sure there are many other interesting examples as you dig into web payments, databases, etc.

What is 64-bit floating point?

It is a number format used by computers. It is also known as double-precision floating point. It takes 8 bytes (or 64 bits) in a computers memory.

That 64 bits is split into three parts - 1 bit for the sign, 11 bits for the exponent and 52 bits for the fraction.

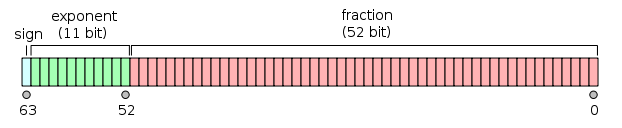
Source: wikipedia.org

Let’s break this down further:

• The sign represents whether the number is positive or negative. If it is 0, the value is positive. If it is 1, the value is negative.

• The exponent indicates how many digits left or right the floating point should be shifted. This type of exponent is called a biased exponent. It takes information from the fraction in order to scale up or down the final result.

• The fraction (sometimes also called the significand or mantissa) represents the binary digits of the number.

  • It can represent whole numbers or decimal values, but they will share the 52 bits. The space at which whole numbers and decimal values exists floats up and down the 52 bits — hence the name floating point.
  • The whole numbers are represented in binary using 2^x and the decimals are represented using 2^-x (or ¹⁄₂^x).
    

Before we get to our test cases, I’d recommend the following resources:

• Vaidehi Joshi’s blog post, Bits, Bytes, and Binary. It is an incredible resource for demystifying binary numbers. I highly recommend her whole BaseCS series. But, be sure to start with this post!

• Bartek Szopka’s talk, Everything you never wanted to know about JavaScript numbers. In addition to being a great talk, there is information on how JavaScript represents numbers in special cases that I didn’t mention above.

• Dr. Axel Rauschmayer’s blog post, How numbers are encoded in JavaScript. This post and his chapter on numbers in Speaking JavaScript are a deeper dive into the number system than I will attempt to cover in this post.

The Test Cases

Test Case One:
1000000 x 1000000 = 1000000000000

A million multiplied by itself is a lot. However, JavaScript provides a Number.MAX_SAFE_INTEGER constant equal to 9007199254740991. And 9007199254740991 is greater than 1000000² (or a million multiplied by a million).

> 1000000 * 1000000
  1000000000000

> 1000000000000 < 9007199254740991
  true

But, if JavaScript only has 64-bit floating point numbers, why are we talking about a max integer value?

JavaScript does only have one number type, but integers can be represented in 64-bit floating point up to 52 bits (with 1 bit for the exponent). If the number changes through an operation, it may not be an integer any longer. Additionally, when using bitwise operators, you may artificially limit your integer value to 32 bits.

Two simplifications we can make:

1. An integer is a number without a decimal and will be represented in 64-bit floating point behind the scenes.

2. As long as you’re working with integer values less than Number.MAX_SAFE_INTEGER and greater than Number.MIN_SAFE_INTEGER, you’re going to get a consistent result.

If you’re working with values close to or larger than the max integer value or smaller than the min integer value, you can either check your input value against the constants (Number.MAX_SAFE_INTEGER or Number.MIN_SAFE_INTEGER) or use a library that specializes in working with arbitrarily large numbers.

---

Test Case Two:
0.1 + 0.2 = 0.30000000000000004

The tricky part of this expression is that it seems like a trick. Where did the 4 come from? Something I hadn’t considered until I spent an afternoon converting numbers to binary and back is that it probably wasn’t intended to be a 4.

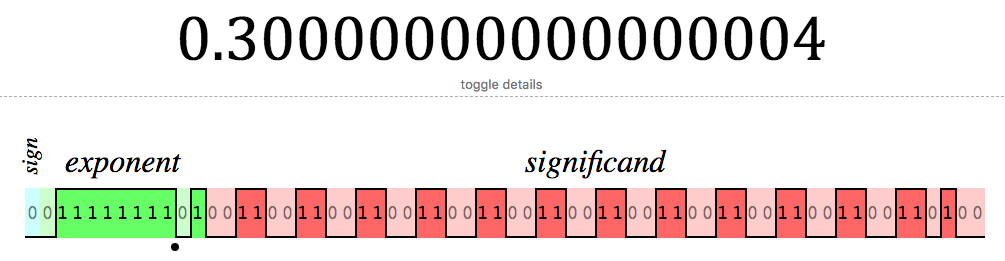
Above is the IEE 754 representation of our results.
Now, let’s investigate this hunch:

100 in binary is 4. 
2² = 4, 4–4 =0, our binary represents the places filled by 2² 2¹ 2⁰

In JavaScript numbers, generally, any digits that exceed the 52 bits provided by the fraction (or significand) are assumed to be 0 and discarded.

Numbers entered into JavaScript are decimal floating-point numbers and are then internally represented as binary floating-point numbers. That conversion for decimal floating-point numbers whose prime factors include anything other than 2 will lead to imperfect results.

For example:

0.125 in decimal = 125/1000 = 1/8 = 0.001 in binary
0.1 in decimal = 1/10 = 1/2*5
0.2 in decimal = 1/20 = 1/2*2*5

And as we discussed before, the decimal values in our binary representation are defined using 2^-x (or ¹⁄₂^x). However, if there is no way to cleanly find a exponent that our number goes into we’ll continue to get back decimal/fraction results until we run out of bits in our internal representation.

When the conversion exhausts its bits, it’ll store the result. Which in this case ends in 100 in binary or 4 as a decimal value.

Summary

• JavaScript has one number type.
• It’s called 64-bit floating point.
• It is defined by the IEE 754 standard.

It is pretty nice, except if you’re a decimal whose factors are anything other than 2 or if you are a number with more than 16 digits.

To avoid exceeding the bits provided to we can compare our input against Number.MAX_SAFE_INTEGER and Number.MIN_SAFE_INTEGER. To avoid rounding errors with fractions, we can scale up our result to an integer and scale back later on. For example:

0.1 * 10 = 1.0
0.2 * 10 = 2.0 
           3.0/10 = .3

Where to go from here?

Here are a few tools that you can play around with. Otherwise, enjoy your additional knowledge about JavaScript and its number quirks.

• IEE 754 Visualization Tool by Bartek Szopka

• Float Explorer by Dave Herman